O Tractatus de Wittgenstein – Parte 2

Dando sequência aos posts sobre o Tractatus de Wittgenstein, segue a segunda parte. Reitero que caso este texto seja usado em trabalhos de faculdade ou monografias (TCC) que seja citada a fonte:

OLIVEIRA, Rodrigo Silva de – A Lógica da Linguagem, Uma Reconstrução Parcial do Tractatus de Wittgenstein. Monografia defendida na PUCRS. Porto Alegre, 2010.

1.5    Os nomes e o significado

O nome é o limite da análise, é um signo primitivo.
Proposições simples pressupõem que o nome tenha significado.
Assim, elucidar o significado de um nome já pressupõe que ele tenha significado.
Uma proposição na qual um nome não possua significado não possui sentido,
é um contrasenso.

Sabemos que a análise da proposição complexa nos levará às proposições simples que a compõem e que a análise das proposições simples nos levará aos nomes que a compõem, então podemos perguntar: o que constitui o nome? Os nomes são entidades primitivas, que não podem mais ser dissecados. É o limite da análise. Dissemos que o nome designa um objeto de maneira inequívoca no interior de uma proposição. Como, porém, um nome se refere a um objeto, ou seja, como ele possui significado? A proposição simples é a menor unidade lingüística dotada de sentido e os nomes não possuem sentido, só podemos falar do significado dos nomes através de proposições, ao tentar elucidar seu significado usaremos proposições, proposições são constituídas por nomes, elas pressupõem que eles denotem um objeto de forma unívoca, proposições só são compreendidas quando já sabemos o significado dos nomes. Assim, vemos que ao tentar elucidar o significado dos nomes já estamos pressupondo que eles tenham um significado. Dada a estrutura da linguagem, não podemos dissecar os nomes, pois ao tentar fazê-lo já estamos pressupondo que estes designem objetos de maneira unívoca.[1]

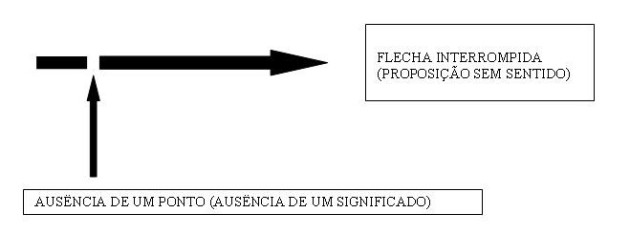
Pode ocorrer em uma proposição de um dos nomes envolvidos não possuir significado, isso é, não designar objeto algum, quando isso ocorre a proposição não terá sentido, será um contra-senso. Uma imagem pode nos ajudar a representar melhor essa idéia: pensemos o nome como um ponto, e a proposição como uma flecha. A flecha é constituída de pontos, pontos não tem sentido, a flecha tem.[2]

Quando um dos nomes que constituem uma proposição não possui significado, isso é, não designa um objeto, a flecha é interrompida e a proposição resultante não possui sentido, é um contra-senso.

Podemos ver claramente que para que uma proposição possua sentido, os nomes envolvidos nela devem significar um objeto, quando falha esse pressuposto a proposição falha em representar uma situação possível, ou seja, não tem sentido. Aqui temos um pressuposto da linguagem. Este é um pressuposto transcendental do sentido, isso é, é uma condição de possibilidade que deve ser satisfeita para que a proposição tenha sentido, para que seja capaz de representar uma situação.

1.6     Situação e Fato

Uma situação é um fato complexo.
Fatos complexos se decompõem em fatos simples
O fato simples é um conjunto de objetos articulados em uma determinada forma.
Fatos são estados de coisas possíveis e podem ser o caso, ou não.

Dissemos que uma proposição representa uma situação possível, mas o que é uma situação? É um objeto? Ou um conjunto de objetos? Uma situação é um fato. Exemplos de fatos são:

A circunstância de eu confiar em Pedro.

A circunstância de haver 50 livros em uma estante.

A circunstância de João morar em uma determinada cidade.

Fatos assim como proposições podem ser simples e complexos. Os exemplos dados acima são fatos simples. Segue alguns exemplos de fatos complexos:

A circunstância de o atual imperador do Brasil ser mulherengo e corrupto.

A circunstância de Pedro saber falar português e inglês.

A circunstância de Pedro morar em uma determinada cidade e gostar dessa cidade.

Fatos complexos são constituídos de fatos simples e a análise de um fato complexo sempre levará aos fatos simples que o compõem. Exemplo:

A circunstância de Platão dar aulas de filosofia e de matemática na Academia e gostar de dar aulas dessas duas matérias.

Podemos decompor este fato complexo nos seguintes fatos simples:

Lápide de Wittgenstein em Cambridge

(1) A circunstância de Platão dar aulas de filosofia na Academia.

(2) A circunstância de Platão dar aulas de matemática na Academia.

(3) A circunstância de Platão gostar de dar aulas de filosofia.

(4) A circunstância de Platão gostar de dar aulas de matemática.

O fato complexo se decompõe em fatos simples e estes, por sua vez, são constituídos por um conjunto de objetos articulados em uma determinada forma. Objetos sem uma articulação não constituem um fato. Assim, quando analisamos um fato iremos de fatos complexos para fatos simples, e de fatos simples para os objetos que o constituem.

Um fato é uma situação possível, ele pode ser o caso ou não. A circunstância de São Paulo ser a capital do Brasil é um fato, uma configuração de objetos possível, mas este é um fato negativo, isso é, que não é o caso. A circunstância de Brasília ser a capital do Brasil é um fato positivo.

1.7 Proposições e fatos

A proposição é um fato.
A proposição simples representa um fato simples.
Comparando uma proposição com a realidade, podemos saber se ela é
verdadeira ou falsa.

Uma proposição é um fato.[3] Nela temos objetos articulados em uma determinada forma. Trata-se de um fato que usamos para sinalizar outro fato. A proposição simples é um sinal de um fato simples. Ela descreve um fato simples e proposições complexas descrevem um fato complexo. Chamamos um fato complexo de situação. Se o fato descrito por uma proposição for o caso, ela será verdadeira; se não for o caso, ela será falsa. Assim, a proposição nos mostra como estão as coisas no mundo se for verdadeira. Dissemos antes que o sentido de uma proposição é a situação possível que ela representa, podemos dizer que seu sentido é o estado de coisas possível que ela representa. Para saber se uma proposição é verdadeira ou não devemos compará-la com a realidade. Nenhuma proposição legítima é verdadeira a priori, isso é, independente dos fatos.[4]

1.8 O sentido da proposição complexa

A proposição complexa é uma função de verdade de proposições simples.
O sentido da proposição complexa é dado pela articulação das proposições
simples que a compõem.
Uma proposição complexa é uma função de verdade de proposições simples.
As proposições simples são funções de verdade de si mesmas.
Todo o trabalho de representação do mundo é feito pelas proposições simples,
as proposições complexas
não representam mais do que as proposições simples que as compõem.

Dissemos que uma proposição simples possui sentido porque ela representa um fato, que seu sentido é o fato possível que ela representa. Como ela consegue fazer isso é algo que mostraremos mais tarde. Como a proposição complexa possui sentido? Qual a relação entre o sentido da proposição simples que a constituem e o seu sentido? Como articulamos proposições simples para formar proposições complexas?

Casa que Wittgenstein projetou e ajudou a construir para sua irmã.

Articulamos proposições simples em proposições complexas através de uma operação lógica chamada operação de verdade ou uma função de verdade, essa operação é o que deve ocorrer com uma determinada proposição para que através dela se construa outra. Essa operação só pode ser aplicada pressupondo as proposições simples, elas não dissecam proposições simples. Para que seja efetiva ela pressupõe as proposições simples e que estas tenham um sentido definido.

Vejamos os seguintes exemplos de proposições simples:

(p) Platão dava aulas de filosofia na Academia.

(q) Platão dava aulas de matemática na Academia.

Como são proposições autênticas descrevem fatos possíveis e podem ser verdadeiras ou falsas. Iremos pressupô-las como dadas e aplicar sobre elas a operação de verdade ou a função de verdade. Iremos representá-las por p e q.

A primeira função de verdade que vamos apresentar é a negação, representada por “~”. Se aplicarmos essa operação sobre p teremos a seguinte proposição: “não é o caso de que Platão dava aulas de filosofia na Academia.” O que a operação de negação faz? Sabemos que p é uma proposição simples autêntica, que tem um sentido definido. A operação de negação altera o sentido de p? O que a operação de negação faz é o seguinte: ela torna ~ p (lê-se não p) falsa quando p for verdadeira e p falsa quando ~ p for verdadeira. O sentido de ~ p depende do sentido de p. O que a operação de negação faz é trabalhar sobre o sentido de p. Pelo exemplo podemos ver que ~ p é obtida de maneira lógica de p, uma vez que a operação ~ p expressa o resultado de uma operação que tem a proposição simples p por base.

Como p admite apenas dois valores de verdade possíveis, V ou F, podemos representar a operação de negação da seguinte forma:

P	~ p
V	F
F	V

O que a tabela, que chamaremos de tabela de verdade, nos mostra é que quando a proposição simples p é verdadeira (coluna 1, linha 1), ~ p é falsa (coluna 2, linha 1) e que quando p é falsa (coluna 1, linha 2), ~ p é verdadeira (coluna 2, linha 2).

O que devemos enfatizar é que a operação não caracteriza o sentido da proposição, ~ p é obtida de maneira lógica de p. O que ~ p expressa é o resultado de uma operação que tem p como base. Dizer que a operação não caracteriza o sentido da proposição é dizer que as proposições complexas não representam nada além das proposições simples que as constituem. Todo o trabalho de representação do mundo é feito pelas proposições simples. Por isso as proposições simples entram no que chamamos de o pressuposto transcendental do sentido, porque o sentido das proposições complexas é dado pela articulação do sentido das proposições simples. O que queremos dizer com articulação do sentido das proposições simples? Uma proposição complexa é uma função de verdade de proposições simples.[5] Chegamos às proposições complexas aplicando as diversas operações de verdade às proposições simples. Uma proposição simples é uma função de verdade de si mesma, pois sua verdade ou falsidade é determinada pelo estado de coisas que ela representa. A representação do mundo é feita pelas proposições simples. É nesse sentido que dizemos que a aplicação de uma “operação de verdade não caracteriza o sentido da proposição” (WITTGENSTEIN, 2008: pag. 215).[6]

Vejamos a operação de conjunção agora. Uma conjunção é quando fazemos uma afirmação conjunta, quando afirmamos que duas coisas se dão juntas. Por exemplo, quando dizemos: “Platão dava aulas de filosofia e matemática na Academia”. Estamos afirmando que “Platão dava aulas de filosofia na Academia” e que “Platão dava aulas de matemática na Academia”, uma conjunção. Iremos representar uma conjunção de duas proposições quaisquer por p & q (lê-se p e q). Uma conjunção afirma a verdade de p e a verdade de q, assim uma conjunção só é verdadeira quando tanto p como q são verdadeiras. Em todos os outros casos a conjunção será falsa. Como p e q são proposições autênticas, isso é, representam fatos possíveis, elas podem ser verdadeiras ou falsas, admitem dois valores de verdade, V ou F. Podemos representar mediante uma tabela todas as combinações possíveis de valores de verdade de uma proposição qualquer mediante uma tabela de verdade. Digamos que tenhamos duas proposições, p e q por exemplo. Todas as combinações possíveis de valores de verdade de p e q são dadas pela seguinte tabela:

P        Q

V       V

V       F

F       V

F        F

Temos quatro alternativas: 1) p e q são verdadeiras, 2) p é verdadeira e q é falsa, 3) p é falsa e q é verdadeira e 4) p é

Manuscrito de Wittgenstein de 1914

falsa e q é falsa. A regra geral pela qual construímos uma tabela de verdade é a seguinte: dada uma proposição complexa qualquer, o número de combinações possíveis de valores de verdade da proposição complexa é igual a 2 elevado ao número de proposições simples que compõem a proposição complexa (vamos designar por n o número de proposições simples que compõem a proposição complexa). Se uma proposição complexa for constituída por apenas duas proposições simples, por exemplo, então teremos apenas quatro combinações de valores de verdade possíveis, ou de estados possíveis, ou ainda, de configurações possíveis de objetos, pois 2² = 4. Se uma proposição complexa qualquer é constituída por três proposições simples, temos uma tabela com 2³ possíveis combinações de valores de verdade, isso é, 8 combinações possíveis.

Como sabemos todas as combinações possíveis de valores de verdade de p e q e sabemos quando a conjunção é verdadeira, podemos obter a seguinte tabela:

P        Q	P    &    Q
V       V	V    V    V
V       F	V    F     F
F       V	F     F    V
F        F	F     F     F

A tabela nos mostra que, aplicada a p e q, a operação de conjunção só é verdadeira na primeira linha, quando p e q são ambas verdadeiras. O que a operação de conjunção expressa é a verdade de p & q quando p é verdadeira e q é verdadeira. Mas como dissemos antes, isso não caracteriza o sentido de p e de q. A conjunção p & q é o resultado de uma operação que tem “p” e “q” por base. O sentido de p & q depende do sentido de “p” e de “q”. Até mesmo a verdade ou falsidade de p & q depende da verdade de “p” e “q”. Dado isso podemos afirmar que a aplicação de uma operação lógica não altera o sentido da proposição. A operação em si nada enuncia, apenas o resultado da operação expressa algo, mas o resultado depende das proposições que são tomadas como base. Com isso queremos dizer: nenhuma representação é acrescentada às proposições simples para que sejam geradas as proposições complexas. Se a proposição “p” é uma função de verdade de proposições simples, “p” não representa nada que não seja já representado nas proposições simples das quais “p” é uma função de verdade.

Dado o que definimos acima, podemos dar a tabela das outras operações de verdade. A tabela correspondente a operação de disjunção (p ou q), que afirma que dado duas proposições quaisquer p e q, ou p é verdadeira, ou q é verdadeira ou ambas são verdadeira. Assim p v q (lê-se p ou q), que é como iremos representar a operação de disjunção é verdadeira se p é V, ou se q é V, ou se p é V e q é V. A disjunção só é falsa quando p é falsa e q é falsa. Assim temos a seguinte tabela:

P        Q	P     v    Q
V       V	V    V    V
V       F	V    V    F
F       V	F     V    V
F        F	F     F     F

A operação condicional (se p então q – representada por p → q) tem a seguinte tabela:

P        Q	P     →   Q
V       V	V    V    V
V       F	V    F     F
F       V	F     V    V
F        F	F     V    F

A operação bicondicional (p se e somente se q – representada por p ↔ q) tem a seguinte tabela:

P        Q	P    ↔    Q
V       V	V    V    V
V       F	V    F     F
F       V	F     F    V
F        F	F     V    F

As funções de conjunção, condicional e bicondicional podem ser definidas através da operação de negação e da operação de conjunção.

---

[1] 3.263 – “Os significados dos signos primitivos podem ser explicados por meio de elucidações. Elucidações são proposições que contêm os signos primitivos. Portanto, elas so podem ser compreendidas quando os significados destes signos já são conhecidos.”

[2] A analogia com setas e pontos é sugerida pelo próprio Tractatus no aforismo 3.144 – “Situações podem ser descritas, não nomeadas. (Nomes são como pontos, proposições são como flechas, elas têm sentido)”. Nossa imagem é extraída do livro Iniciação ao Silêncio (MARGUTTI 1998: pag. 166).

[3] 3.14 – “O sinal proposicional é um fato”

[4] 2.223 – “Para reconhecer se a figuração é verdadeira ou falsa, devemos compará-la com a realidade.”

2.225 – “Uma figuração verdadeira a priori não existe.”

[5] 5 – “A proposição é uma função de verdade das proposições elementares. (A proposição elementar é uma função de verdade de si mesma).”

[6] 5.25 – “A ocorrência da operação não caracteriza o sentido da proposição. Pois a operação não enuncia nada, apenas seu resultado o faz, e este depende das bases da operação.”